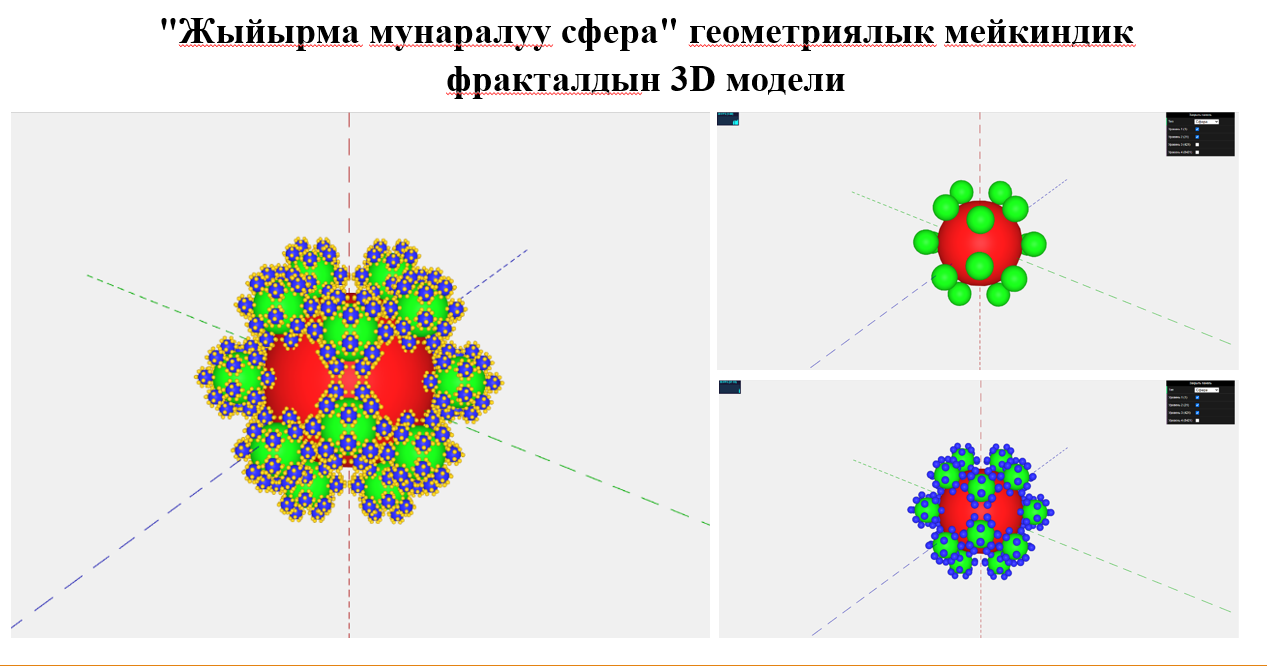
Евклиддик мейкиндикти берилген бөлүштүрүү тарабынан жаратылган бөлүктөп чагылтуунун жана фракталдардын геометриясы
Долбоордун жетекчиси:
Матиева Гулбадан - физика-математика илимдеринин доктору, КРнын Улуттук илимдер академиясынын корреспондент-мүчөсү
Долбоорду алып чыккан факультет:
Математика жана информациялык технологиялар
Телефон номер:
0777009371
Буюртмачы:
ОшМУ
Каржылоо булагы:
ОшМУнун атайын эсебинен
Каржы-н башка булактары (эгер бар болсо):
Сметалык баасы:
3000000
Долбоордун бардык чыгымдар менен баасы:
Зарыл болгон инвестициянын суммасы:
Долбоордун башталышы:
2024-09-01
Долбоордун аякталышы:
2026-08-31
Долбоордун сыпаттамасы
Изилдөөнүн кыскача аннотациясы (актуалдуулугу 200 сөздөн кем эмес): Көп түспөлдүүлүктөрдөгү бөлүштүрүүлөр теориясы жана бөлүктөп чагылтуулар теорияларынын ар бир математикада эле эмес, башка илимдерде да кеңири колдонулушка ээ. Эгерде бөлүктөп чагылтуу берилген бөлүштүрүү тарабынан жаратылган болсо, анда бул аталган теориялар фундаменталдык жактан дагы, колдонмолуулук жактан дагы байышында шек жок. Бөлүктөп чагылтуулар жана бөлүштүрүүлөр теориялары торчолор теориясы менен дагы тыгыз байланышта өнүгүп келе жатат. Эки жана үч ченемдүү торчолор сызыктуу жана сызыктуу эмес толкундар теориясында кеңири колдонушка ээ. Торчо түшүнүгү математиканын, өзгөчө геометриялык маселелерди изилдөөдө жана чечүүдө маанилүү орунга ээ. Бул же тигил торчону тандап (аныктап) алуудан маселенин ийгиликтүү чечилиши түздөн-түз көз каранды. Бөлүктөп чагылтуулар, бөлүштүрүүлөр, торчолор жана фракталдар теориясында Г.Матиева, Н.Н.Курбанбаева, Т.М.Папиева, Ж.А.Артыкова, Г.А.Шамшиева, У.Д.Молдояров, Н.А. Сарыгулова илимий изилдөө иштерин ийгиликтүү жүргүзүп келе жатышат. n-ченемдүү евклиддик Еn мейкиндигинин Ω аймагында p-ченемдүү бөлүштүрүүнүн берилиши менен ага ортоганалдык толуктоочу (n-p)-ченемдүү бөлүштүрүү инварианттык түрдө аныкталат. Ушул бөлүштүрүүлөрдүн ийрилик векторлорунун жардамында аныкталган бөлүктөп чагылтуунун геометриясы Г.Матиеванын эмгектеринде изилденген. Ал эми p жана n-p бөлүштүрүүлөрүнүн бири минималдык болгон жана алардын экөө тең минималдык болгон учурда бөлүктөп чагылтууну аныктоо жана анын геометриясын изилдөө кызыгууну жаратат. Ал эми “фрактал” түшүнүгү бүгүнкү күндө илимдин жана техниканын бардык тармактарына кирүү менен анын колдонулушу болуп көрбөгөндөй кеңири кулач жайып бара жатат. Телекоммуникацияда фракталдар “фракталдык антенна”ларды жасоодо колдонулат. Бул антенналар – электрдик кичи антенналардын жаңы классы болуп, өзүнүн геометриясы боюнча принципиалдык айырмачылыктарга ээ. Фракталдык антенналар радиолокациялык жана телекоммуникациялык системаларды иштеп чыгууда эффективдүүлүктөрүн көрсөтүп жатышат. Фракталдар медицинада рентгендик сүрөттөлүштөрдү анализдөөдө жана гастроэнтерологияда кеңири колдонула баштады. Фракталдык геометрия татаал түзүлүштөрдүн морфогенетикалык закондордун мүнөздөгөндүктөн бул закондор көздүн карегиндеги ооруларды аныктоодо колдонулуп жатат. Фракталдар геологияда жана геофизикада да кеңири колдонулушка ээ. Пайдалуу кен байлыктардын жайланышы фракталдык түзүлүшкө ээ болгондуктан, аларды издөө жана иштеп чыгуу процессинде да фракталдык анализ жардамга келет. Ошондуктан тегиздиктеги (эки ченемдүү) жана мейкиндиктеги фракталдардын жаны класстарын түзүү жана компьютердик технологиялардын жардамында мейкиндиктеги жаңы фракталдардын 3D моделдерин алуу маселеси бүгүнкү күндө актуалдуу маселе болуп эсептелет.
Акыркы 5 жыл ичинде аткарган долбоорлор боюнча маалымат:
Долбоорду изилдөөнүн максаты,милдети жана объектиси: Долбоордун максаты. -ченемдүүлүгү евклиддик мейкиндикти берилген бөлүштүрүү тарабынан жаратылган бөлүктөн чагылтуунун геометриясын изилдөө жана фракталардын жаңы түрлөрүн аныктоо Долбоордун милдеттери - берилген бөлүштүрүүлөрдүн бири же экөө тең минималдык болгон учурда алардын жардамында аныкталган бөлүктөн чагылтууну (n-ченемдүү евклиддик мейкиндикти) изилдөө; - эки жана үч ченемдүү фракталдардын жаңы түрлөрүн табуу жана компьютердик технологиялардын жардамында жаңы табылган мейкиндик фракталдардын 3D моделдерин алуу үчүн программаларды иштеп чыгуу. Долбоорду ишке ашыруунун мүмкүнчүлүктөрү катары төмөндөгүлөрдү белгилөөгө болот: 1) Долбооорду ишке ашырууга 1 илимдин доктору, профессор, 5 илимдин кандидаты, доценттер, 1 PhD докторант, аспиранттар жана магистранттар катышмакчы; 2) ОшМУнун компьютердик базасы.
Долбоордун идеясын ишке ашыруу мүмкүнчүлүктөрү жана изилдөөнүн методу: Долбоорду ишке ашырууда колдонулуучу изилдөө методдору: а) Картандын сырткы формалар методу; б) Кыймылдуу репер методу. в) Г.Ф.Лаптевдин теориялык – группалык методу г) Тензордук метод Сунушталып жаткан долбоор илимдин жана техниканын көптөгөн тармактарында кеңири колдонулушка ээ болуу өзгөчөлүгүнө ээ. Долбоордун темасы докторанттардын, аспиранттарды, изденүүчүлөрдүн, PhD докторанттардын жана магистранттардын изилдөө темалары менен тыгыз байланыштуу.
Долбоордун башка өзгөчөлүктөрү:
Долбоордун темасы боюнча илимий иштердин байланышы:
Изилдөө долбоорунун натыйжасы: Изилдөө долбоорунун натыйжасы - Евклиддик n-ченемдүү мейкиндикти берилген p-ченемдүү бөлүштүрүү тарабынан жаратылган бөлүктөн чагылтуунун касиеттери аныкталат. - Эки ченемдүү жана ченемдүү геометриялык фракталдардын жаңы түрлөрү табылат. - Мейкиндиктеги геометриялык фракталдардын жаңы түрүнүн 3D моделин алуу үчүн компьютердик программалар иштелип чыгылат.
| Файлдын аталышы | Көрүү |
|---|---|
| Матиева Г — 2024.docx |