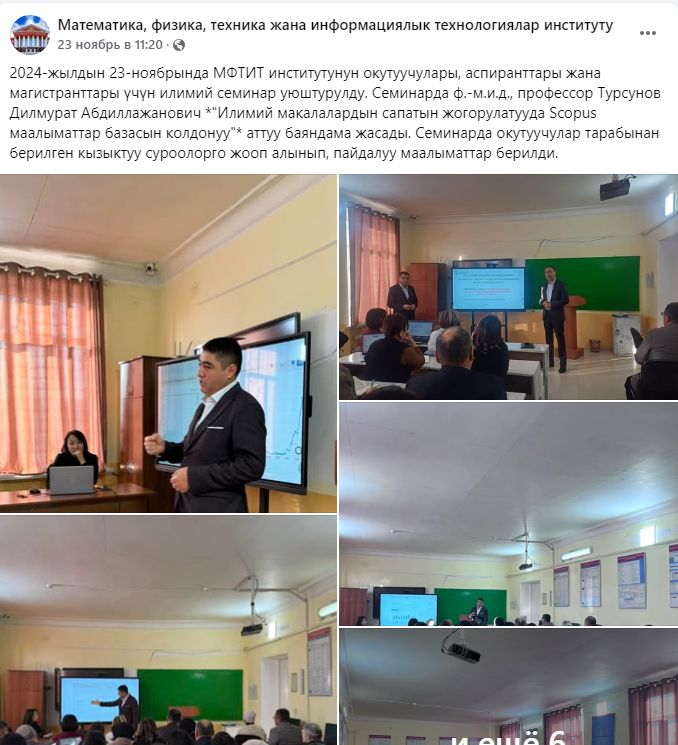
Бисингулярно возмущенные задачи и их применения
Долбоордун жетекчиси:
Турсунов Дилмурат Абдиллажанович
Долбоорду алып чыккан факультет:
ВШМОП
Телефон номер:
+996773299170
Буюртмачы:
ОшМУ
Каржылоо булагы:
ОшМУ
Каржы-н башка булактары (эгер бар болсо):
-
Сметалык баасы:
1000000
Долбоордун бардык чыгымдар менен баасы:
Зарыл болгон инвестициянын суммасы:
Долбоордун башталышы:
2024-01-01
Долбоордун аякталышы:
2024-12-31
Долбоордун сыпаттамасы
Изилдөөнүн кыскача аннотациясы (актуалдуулугу 200 сөздөн кем эмес): Дифференциальные уравнения с малым (или большим) параметром появляются там, где имеются неравномерные переходы от одних физических характеристик к другим. При исследовании подобных задач возникают новые различные явления, поэтому методы асимптотического интегрирования их разрабатываются отдельно для различных классов задач. В связи с этим актуальность результатов исследований по данному направлению не вызывает сомнений. Как нам известно, задачи с двойной сингулярностью, т. е. бисингулярно возмущенные задачи, по сравнению с сингулярно возмущенными задачам, мало изучены. В бисингулярных задачах одна особенность связана с сингулярной зависимостью решения от малого параметра, а другая — с не гладкостью членов асимптотики. Мы исследуем бисингулярные задачи, в которых появляются еще дополнительные особенности, например, промежуточные или дополнительные (пограничный или внутренний) слои. Новизна данного проекта заключается в том, что для бисингулярных задач получить необходимое и достаточное условия существования промежуточного пограничного слоя. В проекте предлагается оригинальный подход, суть которого в том, что вместо универсального метода согласования асимптотических разложений, разработанного и успешно применяемого в научной школе академика А. М. Ильина, используется метод вспомогательной функции, позволяющий получить равномерное асимптотическое разложение для рассматриваемого класса задач с помощью более простой процедуры. Кроме этого, в рассматриваемых задачах будут присутствовать два малых соподчиненных параметра, и мы будем исследовать вопрос, при каких соотношениях этих параметров возникают дополнительные (промежуточные) пограничные (внутренние) слои.
Акыркы 5 жыл ичинде аткарган долбоорлор боюнча маалымат: 1) Фракталдык геометриянын учурдагы маселелери жана евклиддик мейкиндиктеги бөлүктөп чагылтуулардын геометриясы; 2) Развитие PhD докторантуры в Кыргызстане.
Долбоорду изилдөөнүн максаты,милдети жана объектиси: Интерес исследователей к бисингулярным задачам вызван тем, что, с одной стороны, соответствующее направление науки имеет чрезвычайно важное значение в приложениях, а с другой - для решения соответствующих задач существует различные теорий, не дающих полного ответа. Движение вязкого потока, будь то воздух, вода или кровь в наших сосудах, практически всегда связана с эффектом пограничного слоя. Целю исследования является найти достаточные и необходимые условия существования промежуточного пограничного слоя для бисингулярных задач первого и второго порядков. Построить полные равномерные асимптотические разложения бисингулярных задач с промежуточным пограничным слоем. Объектами исследования являются линейные неоднородные обыкновенные дифференциальные уравнения первого и второго порядков, а также эллиптические уравнения второго порядка с двумя независимыми переменными.
Долбоордун идеясын ишке ашыруу мүмкүнчүлүктөрү жана изилдөөнүн методу: Участники проекта имеют опыт в данной научной направлении. Данный проект является продолжением исследований бисингулярных задач и их приложений в физике, технике и в др. областях науки. Методы исследования: асимптотические методы, метод пограничных функций Вишика-Люстерника-Васильевой-Иманалиева, обобщенный метод пограничных функций, метод дифференциальных неравенств, принципа максимума, метод интегральных неравенств, метод малого параметра, методы интегрирования дифференциальных уравнений.
Долбоордун башка өзгөчөлүктөрү: В проекте исследуются бисингулярные задачи с бипограничными слоями - новое направление в теории сингулярных возмущений.
Долбоордун темасы боюнча илимий иштердин байланышы: Научные темы/исследования аспирантов (Садиева А.С., Сулайманов З.М., Бекмурза уулу Ыбадылла, Омаралиева Г.А.) и PhD докторантов (Сабиржанов М.Т., Кожобекова П., Жалилов А., Бекназаров Н.) связаны с темой предлагаемого проекта.
Изилдөө долбоорунун натыйжасы: Защита кандидатских и PhD диссертаций. Публикация научных статьей, в научных журналах цитируемых в базах Scopus и Web of Science.
| Файлдын аталышы | Көрүү |
|---|---|
| Турсунов ДА.pdf |





















.jpeg)